図のような八つの等脚台形に分割された正六角形がある。この正六角形を、赤、青、黄色の３色を使って、互いに接する等脚台形が必ず異なる色になるように塗り分ける方法は全部で何通りあるか。
　ただし、回転させると同じ塗り方になるものは、１通りと考える。




　　
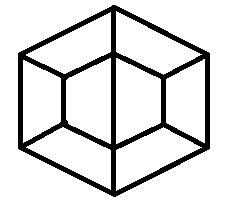
　この問題は、平成14年に国家公務員�T種試験で出題された問題です。
　説明のために、番号を振っておきましょう。


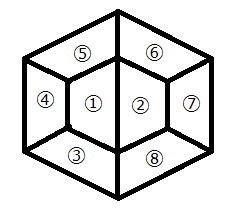
　場合の数の問題とは、条件を満たす場合が何通りあるのかを数えていくのですが、どこから考えるかの決定が最も大切です。この問題でも�@〜�Gのどこから考えるかで手数のかかり方が全く異なります。
　問題文に、「接する等脚台形が必ず異なる色」と書かれているのですから、接するものの多いところから決めていくと、他が多く絞られていくことが分かりますよね。そして、図より接するものが多いのは明らかに�@と�Aです。
　ここで、�@を場合分けして、次に�A、・・としても求まるのですが、この問題のもう一つの重要条件「回転させると同じ塗り方になるものは、１通りと考える」がありますので、�@と�Aの組合せについて一気に場合分けをしましょう。その方がかなり楽になります。まとめられるところはまとめて考えるべきです。
　たとえば、(�@・�A)が、(赤・青)と(青・赤)は、180°回転させると同じ塗り方になります。　よって、これらをダブルカウントしてはいけないと問題が言っているのですから、(�@・�A)の組合せは、(赤・青)、(青・黄)、(黄・赤)の３通りでよいのです。これでモレ・ダブりなしです。

　次に�B〜�Gを考えていくのですが、上記の３通りのどれで考えても場合は同じになるはずですから、ここでは(�@・�A)が(赤・青)の場合で考えてみます。
　赤の�@に接しているのは�B〜�Dです。だから、�B〜�Dは青か黄なのですが、�B〜�Dも隣とは異なる色のはずなので、(�B・�C・�D)の組合せは、A(青・黄・青)かB(黄・青・黄)の２通りに決まります。
　同じように、(�E・�F・�G)の組合せは、C(赤・黄・赤)、D(黄・赤・黄)の２通りです。
　
　ここで注意すべきは、�B〜�Gの組合せは２×２＝４としてはいけないということです。�Bと�G、�Dと�Eが同じ色ではダメだからです。この中では、B−Dの組合せがまずいことになります。よって、�B〜�Gの組合せはA-C、A−D、B−Cの３通りになります。

　最後に全体の場合の数を求めます。
　�@・�Aの組合せ１通りあたり、�B〜�Gの組合せが３通りあるのですから、
　３通り(�@・�Aの組合せ)　×　３通り(�B〜�Gの組合せ)　＝　9通り
　
　　　答えは２になります。

　もしかしたらよく分からないので片っ端から数えようとしてしまう方もいらっしゃるかもしれません。しかし、そうすると時間がかかるだけでなく、数え漏れが頻繁に発生すると思います。どうしても分からない場合の最後の手段くらいにしておきましょう。
　場合の数は、通常、場合分けが必要です。そして場合分けは、どこから分けていくと他がたくさん決定できるか(楽チンか)を常に念頭において攻めるポイントを決めましょう。実はここで勝負がつくのです。ではまた。